Working with Cranky Op-Amps

Introduction

Many people these days get their introduction to audio electronics by using docile op-amps like the Burr-Brown OPA132. This chip is relatively slow at 8 MHz, which is fast enough to pass a low-distortion audio signal, but not so fast that you can easily get into trouble. Also, it has FET inputs, which means that you do not have to worry about the value of the resistors around the op-amp affecting its performance in surprising ways.

There are many other op-amps that are good for audio which are raging tigers by comparison to the OPA132. I wrote the first version of this article after trying to drop a National Semiconductor LM617x into a CMoy pocket amp. It didn't work correctly at all. It oscillated like mad, and had high DC offset at the headphone output. This article explains why these two things happened, and what you can do to fix them. Along the way, you will gain a greater understanding of “real” op-amps, as opposed to the near ideal op-amp behavior exhibited by docile chips like the OPA132. I use the LM617x as my prime example simply because this chip is commonly used for audio, yet it's an extreme mismatch to the stock CMoy design, so it illustrates the problems clearly. That said, the principles are relevant for a great many other chips.

High DC Offset

The Source of the Problem

It's easiest to make integrated circuits using just one kind of transistor. Traditional op-amps are made entirely of bipolar transistors. (Plus some passive components.) The first really popular IC op-amp was the µA741, introduced way back in 1968, yet still available today. Take a look at the schematic on page 2 of the µA741 datasheet, and you'll see that each of the op-amp's input pins is connected to a bipolar transistor's base. We say that this is a bipolar input op-amp.

Why is this significant? One of the characteristics of a bipolar transistor is that they require a small but substantial base current to operate. This current either flows into or out of the op-amp's inputs, and so forces a voltage across the resistors around the op-amp. (Whether the current flows in or out depends on the structure of the op-amp's input stage, but since a negative offset is just as bad as a positive offset, we can ignore this fact.)

Now take a look at page 3 of the National Semiconductor LM617x datasheet. There you will find a spec for “input bias current,” which is this base current. For the LM617x, this can be as high as 4 µA. That's a pretty tiny current, but consider what happens when you force this current across the relatively high resistor values at a CMoy amp's inputs. Ohm's Law tells us that if R2 is 100 kΩ, forcing 4 µA across it will develop a voltage of 0.4 V. Hmm! Now we're talking about something significant. Okay, what happens at the other input? From the DC perspective, the resistance at a CMoy amp's inverting input is R3 and R4 in parallel. Using the default values of 1 kΩ and 10 kΩ, the parallel resistance is 909 Ω. If you force 4 µA across that, you get only 2.7 mV. The offset at the noninverting input is so much higher than at the inverting input that it's close enough to the truth to say that there's 0.4 V of DC offset at the CMoy amp's input with this configuration. When you multiply that by the amp's gain, which is 11 in this instance, you get 4.4 V at the op-amp's output. This much DC offset will kill headphones very quickly.

(Aside: There are two other op-amp parameters that also affect output offset voltage: input offset current and input offset voltage. This article ignores those two because the input bias current is the biggie in typical applications. Considering the others wouldn't change the conclusions reached in this article. If you want to know more about this topic, I recommend reading section 11.3 of Op Amps for Everyone. If you just want to know the total offset, use my offset voltage calculator.)

Non-Solutions

Obviously the amp's gain isn't helping here, but even if we lower it to 1, we still have 0.4 V of offset. This is still way too high, and lowering the gain to 1 probably isn't practical to boot. Most of the time, we need at least some voltage gain in a headphone amplifier.

We could add an output capacitor to block the DC, but the only capacitors large enough to work in this situation are electrolytics. Electrolytics are the absolute worst quality capacitors made. We tolerate them only because for some things, they're the only thing that will work. Only the most starry-eyed audiophile will tell you that putting electrolytics in an audio signal path is a good idea, if there is some other solution that will work.

We don't have to resort to such ham-handed hackery. We can take a first big step by balancing the input bias currents.

Balancing the Input Bias Currents

If you assume that both op-amp inputs have the same input bias current, the formula for balancing the input bias currents is just the parallel resistor equation for two resistors. Using the part names in the CMoy amplifier, the formula is:

This tells you what R2's value must be in order to null out the DC offset, given the values of R3 and R4.

For your convenience, here's that same equation rearranged to solve for R3 and R4:

   

Imagine what happens if we change R3 to 120 kΩ and R4 to 620 kΩ. These two values in parallel are about 100.5 kΩ, which is about as close to R2's 100 kΩ value as you're going to get using the common 5% resistor values. Now the inverting input's offset voltage rises to 0.40216 V. Subtracting that from the offset at the noninverting input and multiplying by the new gain (6.2) you get a tolerably low DC offset of 13 mV. You could try for a lower value by looking for R3/R4 values in the tighter 1% line to get even closer to 100 kΩ, but that quickly becomes a fool's game. The actual input bias current will vary due to manufacturing differences, and the two currents won't be identical. (This is what the op-amp's input offset current spec tells you, by the way.) Also, there are other sources of input-related DC offset that will eventually swamp your efforts at fixing this one type. Finally, even if you take care of everything else, resistor tolerances will still prevent us from completely nulling the offset. In practice, there are more effective ways to attack the remainder of this problem than fine resistor matching.

(Aside: With that background, you're prepared to understand one reason FET input op-amps exist: FETs do not have this high base current. A FET input op-amp can have an input bias current over a million times lower than an LM617x! This is why you do not have to worry about offset from imbalanced input bias currents when using FET input op-amps in headphone amplifiers. The consequence of this is that because it's harder to manufacture an IC with two entirely different types of transistors, FET input op-amps are more expensive than bipolar types, feature for feature.)

New Problem 1: The Input Filter

For me, the acceptable limit for DC offset in headphone amplifiers is 20 mV, so 13 mV is fine. Unfortunately, the input bias current isn't the only source of DC offset at the output of an op-amp. Add in these other sources, and it's easily possible to go over this limit. We need to lower the input bias current imbalance component of the DC offset a bit more yet.

One way you might think to improve on this is to lower the resistor values around the op-amp inputs. Let's do something drastic and cut all three resistors in question to one tenth the values I used above. This cuts DC offset by a factor of 10, too. Voilá, problem solved, right?

Well, yes, but you've just created a new problem.

In a CMoy amplifier, R2 and C2 form an RC high-pass filter. This kind of filter passes high frequencies, and cuts low frequencies. The most important number describing such a filter is its “corner frequency.” For a high-pass filter, attenuation increases by a steady 6 dB per octave below this frequency, and it flattens off asymptotically toward zero above this point. The corner frequency happens to be the point where attenuation is 3 dB, so some people will also call this “the -3 dB point,” but the actual value isn't important in practice.

The formula for an RC filter's corner frequency is:

With the original CMoy values, the corner frequency is about 16 Hz. So, the attenuation is 3 dB at 16 Hz, 9 dB one octave down at 8 Hz, 15 dB down at 4 Hz, etc. This shows another way to look at the DC blocking nature of the CMoy amp's input capacitor: at DC, this filter has infinite attenuation.

But we just decided to cut R2, R3, and R4 by a factor of 10 to lower DC offset. What did we do to this filter? The corner frequency is now 10 times higher, 160 Hz. We just completely destroyed the amp's bass response! To get our filter characteristic back, we need to raise the value of the input capacitor by the same factor as we lowered the value of the resistors.

The standard input capacitor for the CMoy amp is 0.1 µF, so we need to go up to 1 µF. 1 µF audiophile-quality capacitors exist, so this is doable. But as I describe in the article Input Capacitors for Headphone Amps, 0.1 µF is just barely sufficient to begin with. If you follow the advice in that article, you'd want to use a 1 µF capacitor with Chu Moy's original R2 value. This implies going up to a 10 µF input cap in this new resistor configuration. Film caps this large do exist, but they're expensive and hard to find in DIYer quantities. Furthermore, if it's physically small it will be low quality, or if it's good for audio it will be so large that it probably won't fit in your amp's enclosure to begin with.

New Problem 2: Input Loading

It just isn't practical to go over about 1 µF for headphone amp input capacitors if audio quality is your primary goal. Indeed, your choice of capacitor line and physical layout issues may force you to a 0.47 µF or lower value capacitor. We need to find a better way to fix this DC offset problem.

You might choose to embrace this constraint instead of complaining about it. Instead of trying to get DC offset to vanishingly low levels, let's just try to get DC offset a little lower than our 20 mV threshold value. We'll only cut the resistor values in half, and double the size of the input cap. Since compromise is the game of the day here, we won't try to find a good 2 µF capacitor, but instead settle for 1 µF, or maybe even 0.47 µF. It isn't perfect, but it's not bad.

But now we have another new problem. By cutting the R2 value in half, we're now “loading” the volume pot, if we have one. The general rule of thumb in this piece of the electronics world is that a source should have an impedance at least 10× lower than its load. In the CMoy design, Chu Moy recommended 100 kΩ for R2 because he also recommended a 10 kΩ volume control. If we cut R2 in half, we have to cut the pot's value in half, too. Problem is, there are no good 5 kΩ audio pots to speak of. Even if we could find one, the 10× loading rule applies for the pot as well: it's the load for the audio source. It's not unheard of for audio sources to have output impedances as high as 1 kΩ. For many years, 600 Ω was the most common output impedance value. This is why 10 kΩ is the lowest common audio pot value.

New Problem 3: Resistor Noise

All resistors generate noise, proportionally to the resistor's value. This is called Johnson noise (after its discoverer), and the formula for it is this:

where k is Boltzmann's constant (1.38 × 10^-23), T is the temperature of the resistor (in Kelvins), R is the resistor value, and B is the bandwidth over which you want to calculate the noise. So for instance, the noise of a 1 kΩ resistor at room temperature (300 °K is a nice round number, and close enough) will generate 575 nV of noise over the audio bandwidth (20 Hz to 20 kHz):

This is a property of all conductors, due to thermal effects. (It is also called thermal noise, because of this.) The higher the resistor value, and the higher the temperature, the higher the noise. (You can read more about the phenomenon here. You can play with the numbers using my op-amp noise calculator.)

You can see the problem, then: by going with 120 kΩ and 620 kΩ feedback resistors above, we've increased the circuit noise. Is it a big enough difference to matter? The proposed circuit will have only a -80 dB noise floor relative to a 1V signal, and that ignores the noise contribution from the op-amp itself, and any noise from the source. That's pretty quiet, but audible. The stock CMoy configuration (adjusting to get the same gain) has a noise floor 7 dB lower, which is enough to be perceived as significantly quieter.

Solutions

Okay, so both the pot and the input cap mean we can't lower R2, which forces R3 and R4 to be high in order to balance the input bias currents. Have we completely painted ourselves into a corner? Fortunately, no.

A single-channel op-amp really only requires 5 pins, but we put them in 8-pin packages for historical reasons. Frequently, IC designers will use two of these pins for a DC offset nulling feature. If your chip has such a feature, it's possible for it to trim out small errors. How you use this feature and how large an error it can fix are very much chip dependent. Read its datasheet.

If you're using a dual-channel op-amp, all 8 pins are required just for the core op-amp functions, so you can't use that method. And, sometimes you just cannot afford trim pots for one reason or another. All is not lost.

Another possible fix is to simply avoid bipolar chips with high input bias current. All the major op-amp manufacturers these days offer parametric search engines, where you can specify the maximum input bias current that your design can tolerate. Perhaps you can find an alternate chip that will work. Even better, many times there is a high-grade version of the chip you want to use. Almost always, the entire advantage to these high-grade op-amps is in better DC specs. That may be enough to save your design.

If all that fails, you might start questioning the constraints you've placed on yourself. Do you really need that input capacitor? In another article, I argue that it's often more trouble than it's worth. So let's say we decide that the input cap isn't pulling its own weight. What happens if we remove it? Well, at DC, we now have two resistances in parallel on the noninverting input: the pot and R2. Since the pot's resistance is so much lower than the value of R2, it dominates. This lower value on the noninverting input means we can get away with lower resistor values in the feedback loop. Lower values mean lower DC offsets, and as a side bonus, lower circuit noise. The only trick here is, the pot is a variable resistance. That means DC offset will vary as you turn the volume knob. Depending on the chip you're using, this may be harmless, or it could mean that there are volume settings where DC offset rises to harmful levels. You will have to crunch the numbers to find out if this will work.

The Bottom Line

The amp's gain and the values of the pot, input cap, input resistor, and gain resistors all interact with each other. Lowering any of the resistor values requires that the other two be lowered by the same factor to keep all else equal. That in turn means that the input cap has to be raised by that same factor. Meanwhile, the pot must remain at least 10× lower in value than the input resistor. You'll frequently find that changing one value means the required change in one or more of the others is impractical. This careful balancing act is the soul of engineering. There are no truly perfect solutions in engineering, only holistically acceptable collections of compromises.

Oscillation

Why It Happens

Take a look at the CMoy pocket amp schematic. It's so simple. The voltage from the pot is presented at the op-amp's noninverting input, the feedback resistors tell the op-amp how much gain you want, and the op-amp puts out what you gave it magnified by that gain. So straightforward and neat. Oh, wouldn't it be wonderful if that's how things worked in the real world!

In a real circuit, current doesn't just go from A to B, following the traces laid down on the printed circuit board. Some of it goes across the surface of the circuit board instead, because the surface is never 100% clean. Since PCB material isn't a perfect insulator, some also goes through the PCB material. Current finds other sneak paths past your feedback loop, too, such as nonzero power and ground impedances, parasitic components in the feedback loop, etc. And those are the easy ones. If things are really getting weird, you have still other paths, like RFI through the air.

Why does this matter? It all comes down to op-amp action and phase shift.

The thing that makes an op-amp an op-amp is that it always tries to make its two inputs have an equal voltage. We call this op-amp action. The purpose of adding resistors and such in the feedback loop is to modify this op-amp action.

Let's see how op-amp action works to produce voltage gain. Imagine that we have 0.1 V at the amplifier's noninverting input. Imagine then that this voltage goes straight through the op-amp completely untouched: we get 0.1 V at the output. This voltage goes around the feedback loop, which contains a simple voltage divider in an amplifier like the CMoy pocket amp. For the sake of argument, let's say it's a 10× voltage divider. Our 0.1 V signal is reduced to 0.01 V by this divider. The op-amp wants to make its -IN voltage equal to its +IN voltage, so it raises its output voltage by a factor of 10. Now the output is 1.0 V, which is divided down to 0.1 V by the feedback loop resistors, so the op-amp is happy. We have voltage gain.

Now imagine some force comes along — its nature doesn't matter here — and forces the op-amp's output voltage down a smidge. Through the feedback loop, this forces the inverting input down, too. The op-amp sees that the inverting input is trying to go lower than the noninverting input, so again op-amp action comes into play, forcing the output upward to counteract our mystery force. This is why op-amps have such low distortion and low output impedance when operating in their normal range. Op-amp action forces corrective measures to be taken any time there is a deviation from the expected behavior. The only reason op-amps have distortion at all is that we cannot create perfect op-amp action in the real world.

Okay, so what about the real world, then? Let's imagine what happens if our amplifier is presented with a sine wave instead of a simple DC voltage. Let's also say there is some delay in the circuitry within the amplifier, such that it shifts the sine wave by 180 degrees as it goes through the op-amp. In a sine wave, 180 degrees of shift reverses the voltage: 2 V becomes -2 V, -0.3 V becomes 0.3 V, etc. Let's say that the sine wave has 1 V peaks, and that a positive peak is at the amplifier's input. Due to the delay within the op-amp, that means that the output is only now putting out what happened 180 degrees ago, which is -1 V. For now, we'll ignore gain and put -1 at the inverting input, too. The two inputs are unequal, so op-amp action kicks in to try and correct it. The noninverting input is higher than the inverting input, so the op-amp tries to raise its output voltage a smidge. But because there is 180 degrees of phase shift, this actually results in the output going down by a smidge instead! We have a self-reinforcing cycle called “positive feedback” that forces the output voltage hard one direction, and then because of real world limits it must go back the other way as fast as it can. The cycle repeats endlessly. Congratualations, you have created an oscillator.

So obviously it would be Really Bad^TM to make an op-amp with 180 degrees of phase shift. But in the real world, we cannot make an op-amp with 0 degrees of phase shift. Real op-amps always have some phase shift. The difference between the amount of phase shift and 180 degrees is called the op-amp's phase margin. If nothing else in your circuit adds a delay, you can get away with 0.0001 degrees of phase margin. But life isn't that simple, of course. Remember all those sneak paths I listed above that avoid your carefully planned negative feedback loop? If conditions are right, any of these can set up a positive feedback loop and create an oscillator.

In a real op-amp, phase shift varies depending on frequency. Since real signals like music are composed of many wanted frequencies plus unwanted ones like noise, the way a circuit reacts to a signal can be very complex. A circuit can operate without any oscillation in some circumstances, but if just the right frequency enters into the circuit, it can take off into oscillation.

As a rule, the faster an op-amp is, the less phase margin it will have. Furthermore, wider bandwidth means there are a greater range of signals that the op-amp pays attention to. If you present an 8 MHz amplifier with 21 MHz noise, it's more or less going to ignore it. But if you present that same noise to a 220 MHz op-amp, it will amplify it right along with the rest of your signal. If that magnified noise happens to be of just the right frequency to trigger oscillation, your choice to use a faster chip will be fateful.

How to Fix It, Part 1: Power Supply Bypassing

An ideal power supply has zero impedance. Ohm's Law (V=IR) tells us that if impedance (R) is zero, no amount of current (I) can possibly force a change in the power supply's voltage (V). It would be a perfect voltage source. The same goes for your ground: no amount of current dumped to a perfect ground changes the ground voltage.

In the real world, the power supply and ground always have a nonzero impedance. We try to get as close to zero as possible, but it is not possible to construct a perfect voltage source. This means that your circuit's varying current draw sets up tiny voltage ripples in the power and ground signals. It's easy to see why the stability of the ground path matters: in a CMoy amp, the op-amp's -IN input is connected to ground through R3, so if ground is bouncing, it's like a phantom signal appearing at -IN. As for the power rails, an op-amp doesn't have infinite power supply rejection ratio, so some ripple on the power rails makes it into the op-amp's output, and so can cause oscillation. (See the companion article Op-Amp Power Supply Quality Considerations for more on such topics.)

One way to lower the power and ground impedances is to add bypass capacitors. Capacitors are energy storage devices. When you place them in parallel with a power circuit, the capacitor tries to smooth out any ripples in that circuit. The art of using bypass capacitors is subtle, however. You can't just throw a bunch of caps on the board and expect all the oscillations to go away. The reasons are complex.

First, the opposite of capacitance is inductance, and all wires have inductance. Making wires shorter and thicker reduces inductance, but it has practical limits. Because inductance counteracts capacitance, too much wire between a bypass capacitor and what it is supposed to be bypassing will render that cap ineffective. Therefore, a bypass capacitor should go as close to the device being bypassed as possible. For critical work, you must even consider the length of the capacitor's lead. This is one reason why surface mount technology has become so popular: surface mount ceramic capacitors have essentially zero lead length (hence little inductance) and can sit extremely close to whatever they need to bypass. That multi-gigahertz computer on your desktop wouldn't be possible without the miniaturization afforded by surface mount technology. You simply could not build the same circuit twice the size and have it work: the extra wire length alone would prevent it from working.

The most popular bypass capacitors are 0.1 µF ceramics. For op-amp audio circuits, it's best to add two per op-amp, one from each power rail to ground. The leg going to ground can be as long as it needs to be; get the other leg as close to the power pin as possible. Because the effectiveness of capacitors for bypassing relative to frequency goes up as the value goes down, you may need to go down to 0.01 µF for faster op-amps. You can also use film capacitors instead of ceramics. Ceramics are better at high frequency, but films have higher linearity, which makes audiophiles happy. The linearity is of no value if the circuit doesn't work because the bypass capacitor is ineffective at the problem frequency, however, so don't rule out ceramics. A nice compromise is the C0G or NP0 type ceramic, which has nearly as high a linearity as a film cap but has the high speed advantages of a ceramic.

Also helpful can be some larger tantalum capacitors. They don't handle the higher frequency noises, so they don't have to be as close to the chip as the ceramics. As with the ceramics, it's better in analog circuits to use two caps from ground, one going to each power rail. But, you might get away with using just one from rail to rail. Values somewhere in the 1 µF to 10 µF range work best. You can let one big tant (or a pair of them) serve several ICs. Bigger is better, especially if each IC doesn't have its own tant(s), but don't get crazy. A 2.2 µF bypass cap might serve just as well as a 10 µF in a situation where 1 µF would be insufficient.

How to Fix It, Part 2: Bandwidth Limiting

You'll recall that one of the factors increasing the risk of oscillation is excess bandwidth.

If you listen to hard-assed electrical engineers, they'll tell you that even the lowly µA741 is good enough for audio. They're right that it has enough bandwidth, and sufficient slew rate to pass a decent audio signal, as long as you don't load it down too heavily. But if you listen to your headphones instead of those engineers, you will hear something very different: the µA741 sucks for audio!

When we use a modern high-speed op-amp like the 100 MHz LM617x for audio, it's not because we need to amplify signals beyond the 20 kHz audio bandwidth or because we need unholy fast slew rates. What we're more after are things like the chip's higher precision and its ability to drive low impedance loads. Chips with a wide closed-loop bandwidth also tend to have a wide region of flat open-loop bandwidth, which means the feedback factor is linear over a wider range of the audio bandwidth. These and other features add up to lower distortion in that critical lower 20 kHz.

It's possible to have our cake and eat it, too. If you drop a small capacitor across the feedback resistor (R4 in most of the amps discussed on this site), the gain of the amp starts dropping as the frequency rises. (You can use the RC filter equation above to determine this filter's -3 dB point.) Since voltage gain is almost always a factor in the onset of oscillation, this bandwidth limiting cap — also called a phase lead cap — can cure oscillation.

Let's work an example. Say your R4 is 620 kΩ. Let's try a 10 pF bandwidth limiting cap. The RC filter formula above tells us that the op-amp will be acting like an RC filter with a corner frequency of about 26 kHz with these values. (In other words, the amp's gain is reduced by 3 dB from its nominal value at 26 kHz.) That's not far above the audio bandwidth, so we might choose a slightly smaller cap value, or we might somehow finagle smaller resistor values to allow us to use a larger cap value. Putting the corner frequency somewhere in the 30 kHz to 100 kHz range is probably best.

Since this cap is directly in the audio path, quality matters. The absolute best caps for audio use are polypropylenes, but the smallest I've ever seen are 33 pF, and those are hard to get. Next best are polystyrenes, which are made in all values suitable for this purpose, but they, too, are hard to get. The third best choice isn't bad at all, and they're pretty easy to find: silver mica. If you cannot get those, or you cannot afford the board space they take, there's only one level lower you should ever go here: you can use NP0 or C0G ceramic capacitors. (These two types are the same.) Never use any other ceramic type in the audio path. Never, never, never. Change the circuit another way to avoid oscillation before you break down and use, say, an X7R ceramic in the audio path. Only film types and NP0/C0G ceramics are linear enough for high quality audio.

There is an important situation where a bandwidth limiting cap will make things worse instead of better. Because a bandwidth cap rolls off the amp's gain toward 1 at high frequencies, it doesn't work correctly with op-amps that aren't unity gain stable. For instance, the NE5534 requires a gain of at least 3 to be stable. Using a bandwidth limiting cap with such an op-amp will frequently create an oscillator.

How to Fix It, Part 3: Things to Try Before Resorting to Voodoo

If the op-amp still oscillates, try these things, in this order:

1. Add a small resistor to the op-amp's output, either inside or outside the feedback loop. (10-100 Ω) This isolates the op-amp from any load capacitance. I prefer putting it inside the feedback loop, because op-amp feedback will counteract some of the bad effects of having the resistor, yet the resistor will remain effective. Others recommend putting it outside the loop, so that it can protect both the OUT and the -IN op-amp pins. This raises the amplifier's output impedance, though, which is not without consequences.

2. Do the same as in the previous step, except use a ferrite bead or chip ferrite instead of the resistor. At low frequencies, the resistance of a ferrite is basically that of the wire going through it. The resistance rises as frequency rises, and it's at high frequency that oscillation usually occurs. Thus, you get the output resistance you need at the oscillation frequency, while having very low resistance at audio frequencies. This can make it more palatable to put the ferrite outside the feedback loop; with standard ferrite beads, it's easy to just put a bead around each wire going to the output jack. I make an exception when using chip ferrites, since the small wires used in them make the DC resistance significant; therefore, I only use them inside the feedback loop, so feedback can remove its effect at low frequencies.

3. Raise the amp's gain a bit. Unlike the feedback capacitor trick, this truly limits the bandwidth of the op-amp. If you look in your op-amp's datasheet, you'll find a spec called “gain-bandwidth product” (GBP). This spec comes from the fact that gain and bandwidth have a linear relationship in an ideal op-amp, such that multiplying gain by bandwidth always equals the GBP. (Practical op-amps have nonlinearities in their gain and bandwidth relations, so there is usually a graph of the actual gain vs. bandwidth curve in the datasheet.)

4. If you have control of the circuit board's layout, it may be possible to improve the layout enough to fix the oscillation. Tips on improving your layout are beyond the scope of this article, however.

5. If you're using a socket, solder the op-amp chip directly to the board instead. This lowers parasitic inductance, so the bypass caps work better. It also reduces the parasitic capacitance between the op-amp inputs, which can also be a cause of oscillation.

6. Add a buffer inside the op-amp's feedback loop. (See Figure 4 in the BUF634 datasheet for an example of this.) This relieves the load on the op-amp, which helps most significantly by increasing the op-amp's phase margin. Buffers also tend to be better at dealing with capacitive loads than op-amps. A long headphone cable can easily have 1000 pF of shunt capacitance, which is well beyond the recommended load range for most op-amps.

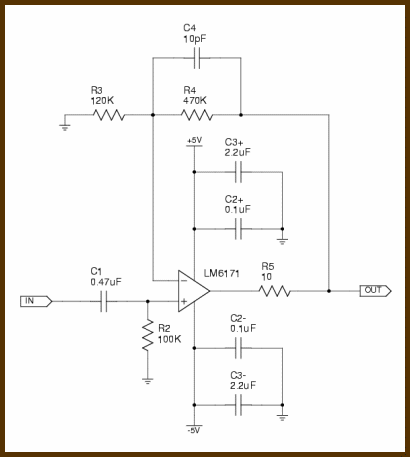
The Completed Schematic

Here's the schematic using Chu Moy's part names, with the additions described in this article: